Физика мягкой материи
Жидкие кристаллы

Мы отслеживаем появление новых жидкокристаллических фаз в экспериментах и строим их теоретическое объяснение на основе данных о теплоемкости, сдвиге температуры перехода в магнитном поле и нейтронных экспериментов про динамику молекул в липидных мембранах. Исследования ведутся в рамках феноменологических моделей, которые являются обобщением теории Ландау и теории упругости для жидкокристаллических фаз и мембран. Кроме того, мы обеспечиваем теоретическую поддержку экспериментальных работ про различные включения (изотропной фазы или островков) в свободно подвешенных смектических пленках.
Ключевые работы:
E.S. Pikina, A.R. Muratov, E.I. Kats, V.V. Lebedev, Nonlinear electro-hydrodynamics of liquid crystals, JETP 137(1), 114-124 (2023); [LINK]
E. Pikina, B. Ostrovskii, S. Pikin, Coalescence of isotropic droplets in overheated free standing smectic films, Soft Matter 16(19), 4591-4606 (2020); [LINK]
E. Kats, V. Lebedev, Landau theory for helical nematic phases, JETP Letters 100(2), 110-113 (2014); [LINK]
Активные среды
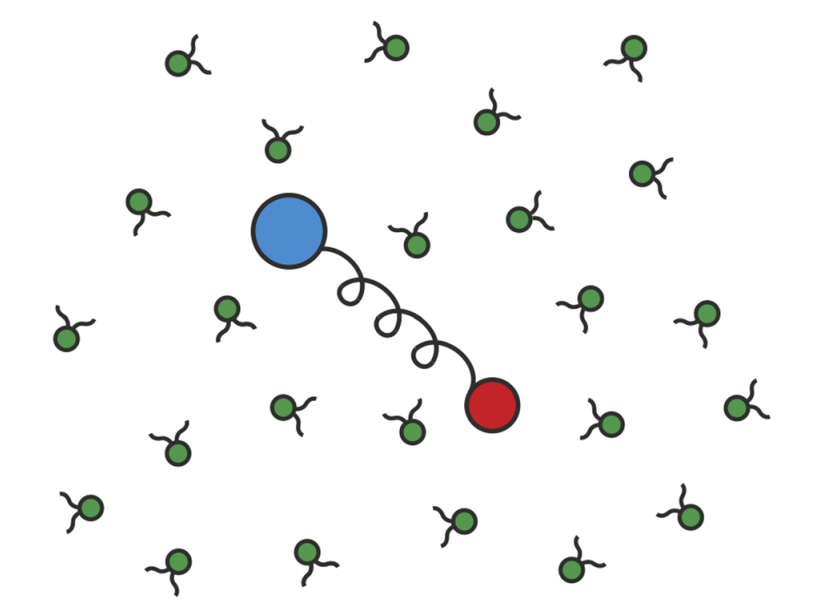
Будучи принципиально неравновесными системами, активные жидкости, такие как суспензии плавающих микроорганизмов или активных коллоидных частиц, проявляют необычные свойства отличные от свойств привычных равновесных сред. Даже при относительно малых концентрациях активные микрочастицы могут создавать сильные флуктуации скорости жидкости, которые сильно-коррелированы во времени и в пространстве и не подчиняются флуктуационно-диссипационной теореме. Мы провели теоретическое моделирование процессов диффузии и направленного движения примесных пассивных частиц в активных суспензиях. Были получены аналитические выражения для коэффициента относительной диффузии пассивных частиц, знание которого позволяет судить о скорости перемешивания примесей в хаотическом течении этого типа, а также для скорости и персистентной длины направленного движения пассивных частиц асимметричной формы.
Ключевые работы:
Биополимеры
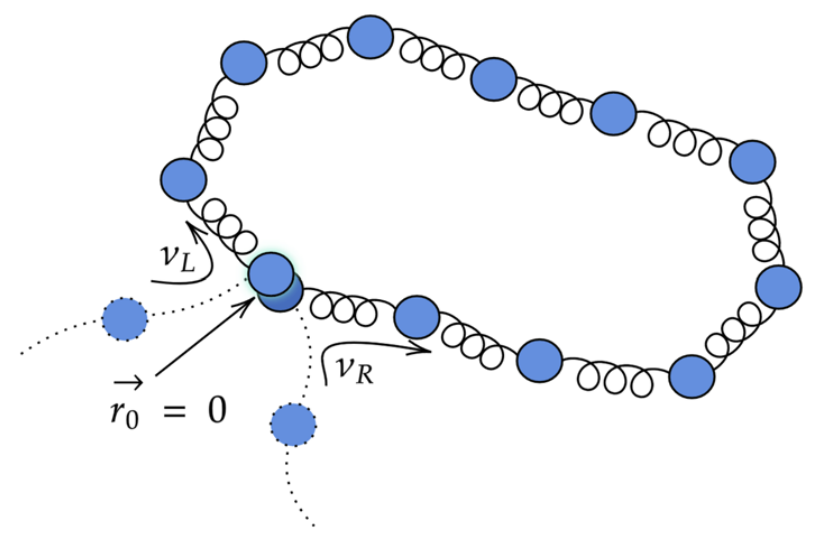
Мотивированные недавними экспериментальными наблюдениями за выпетливанием ДНК белковыми моторами мы исследуем статистические свойства растущих полимерных петель в рамках модели идеальной цепи. Конформация петли статистически характеризуется средним радиусом гирации и вероятностями попарных контактов между звеньями цепи. Оказывается, что один безразмерный параметр, который задается отношением времени релаксации петли к времени, прошедшему с начала экструзии, контролирует переход между почти равновесной и сильно неравновесной асимптотиками в статистике петли, независимо от конкретной зависимости скорости экструзии от времени. Кроме того, мы показываем, что двусторонние и односторонние моторы вытягивают петли с почти идентичными свойствами. Наши предсказания основаны на двух строгих полуаналитических методах, сопровождаемых асимптотическим анализом пределов медленной и быстрой экструзии.
Ключевые работы:
K.E. Polovnikov, H.B. Brandão, S. Belan, B. Slavov, M. Imakaev, L.A. Mirny, Crumpled polymer with loops recapitulates key features of chromosome organization, Phys. Rev. X 13, 041029 (2023); [LINK]
D. Starkov, V. Parfenyev, S. Belan, Conformational statistics of non-equilibrium polymer loops in Rouse model with active loop extrusion, J. Chem. Phys. 154, 164106 (2021); [LINK]