Стохастические процессы
Транспорт частиц вблизи границ
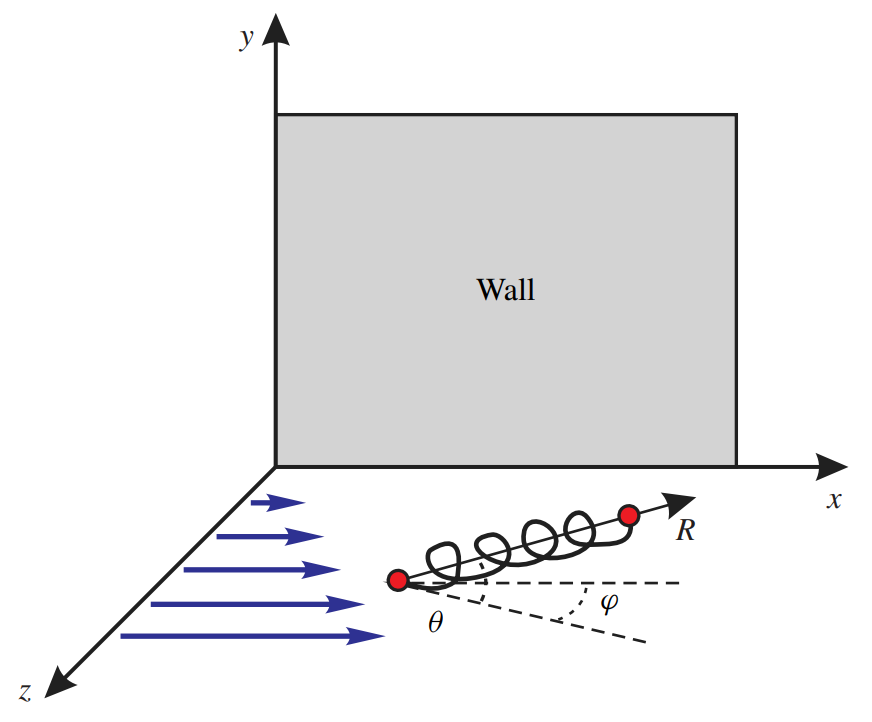
Разработаны теоретические модели процессов турбулентного транспорта тяжелых примесных частиц в пристенной области гидродинамической турбулентности, учитывающие такие физические факторы как: инерционный отклик частиц на флуктуации переносящего их поля скорости, диссипативные столкновения частиц с ограничивающий турбулентный поток стенкой, неоднородность интенсивности пульсаций поля скорости, ненулевое время корреляции турбулентных пульсаций, гравитационное осаждение. В рамках этих моделей были получены аналитические результаты для пространственных распределений конценрации частиц в вязком подслое турбулентного течения вблизи непроницаемой стенки и для скорости осаждения частиц в приземном слое атмосферы. Кроме того, мы теоретически описали статистические свойства пристенных областей хаотических течений, характеризующихся низким числом Рейнольдса, а именно, эластической турбулентности полимерных растворов и стоксова течения в микроканалах с шероховатыми стенками.
Ключевые работы:
Статистика лазерного излучения
Задача о распространении лазерного луча в атмосфере является классической, ей посвящены тысячи работ. Известно, что на больших расстояниях от источника луч разбивается на спеклы за счет рассеяния на флуктуациях показателя преломления среды. Мы интересуемся хвостами функции распределения вероятности интенсивности лазерного луча и учетом эффектом конечности интегрального масштаба турбулентности. Проводится интенсивное численное моделирование.
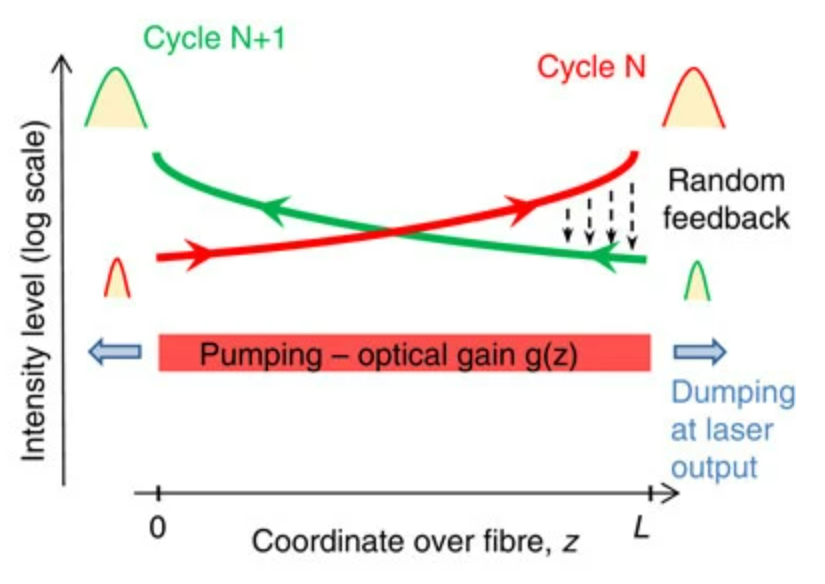
Также мы изучаем статистику выходного излучения случайного непрерывного волоконного ВКР-лазера. Статистика сигнала близка к рэлеевской, а отклонения обусловлены керровской нелинейностью. Для определения статистики отклонений мы находим аналитически средний квадрат интенсивности выходного сигнала, основываясь на кинетической теории. Мы показываем качественное согласие с имеющимися экспериментальными данными и дополняем наши аналитические результаты численными расчетами.
Ключевые работы:
I.V. Kolokolov, V.V. Lebedev, Probability of High Intensities of the Light Wave Propagating in a Turbulent Atmosphere, JETP Letters 118(4), 238-243 (2023); [LINK]
I. Kolokolov, V. Lebedev, P. Lushnikov, Statistical properties of a laser beam propagating in a turbulent medium, Phys. Rev. E 101, 042137 (2020); [LINK]
D. Churkin, I. Kolokolov, E. Podivilov, I. Vatnik, M. Nikulin, S. Vergeles, I. Terekhov, V. Lebedev, G. Falkovich, S. Babin, S. Turitsyn, Wave kinetics of random fibre lasers, Nature Commun. 6, 6214 (2015); [LINK]
Перезапуск
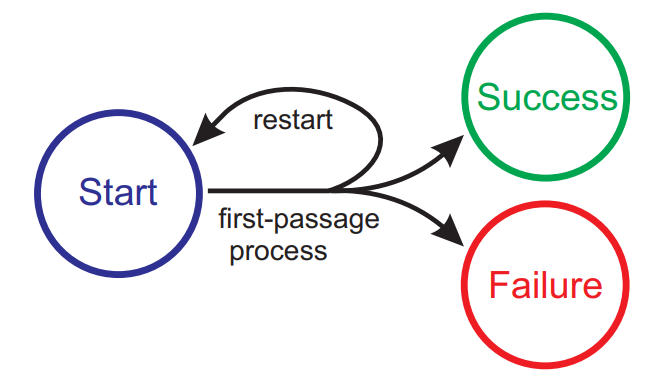
Около тридцати лет назад в теории информатики было продемонстрировано, что перезапуск (т. е. прерывание стохастического процесса с последующим его новым запуском) позволяет сократить среднее время завершения рандомизированных алгоритмов поиска. Много позже аналогичный эффект был обнаружен в рамках теоретических моделей кинетики ферментативных реакций. Далее стало понятно, что помимо математического ожидания времени завершения, перезапуск дает возможность оптимизировать многие другие важные характеристики стохастических процессов. Нами были развиты строгие аналитические методы решения проблемы оптимального перезапуска в контексте оптимизации медианного времени завершения стохастического процесса, модуса функции распределения времени завершения, и вероятности реализации желаемого сценария завершения процесса.
Ключевые работы:
D. Starkov, S. Belan, Universal performance bounds of restart, Phys. Rev. E 107, L062101 (2023); [LINK]
S. Belan, Median and Mode in First Passage under Restart, Phys. Rev. Research 2, 013243 (2020); [LINK]
S. Belan, Restart could optimize the probability of success in a Bernoulli trial, Phys. Rev. Lett. 120, 080601 (2018); [LINK]