Гидродинамическая турбулентность
Когерентные вихри в двумерной турбулентности
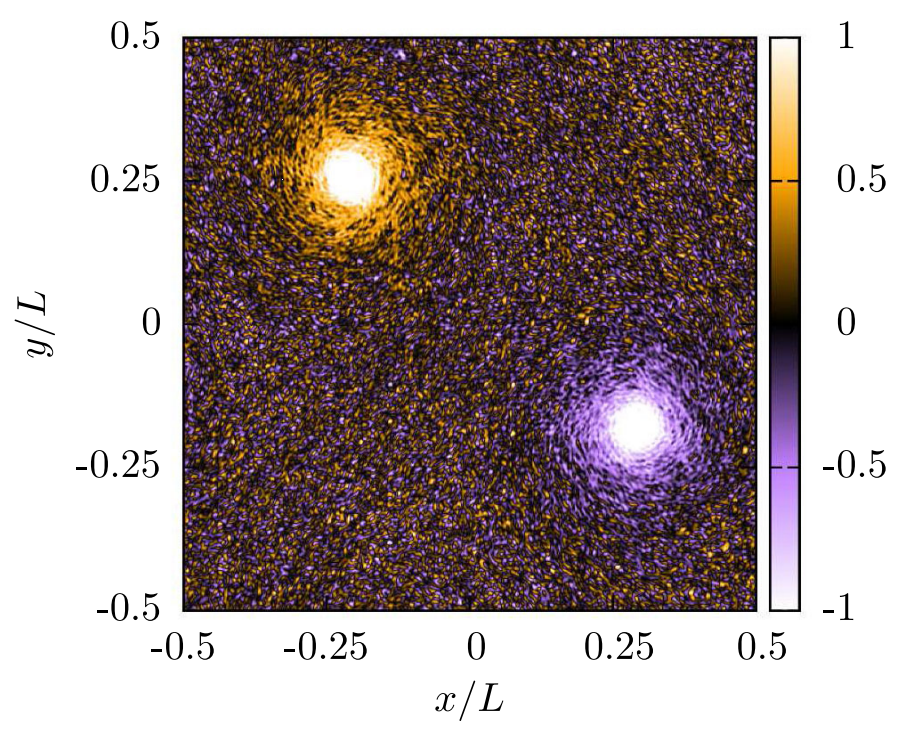
Исследования посвящены изучению свойств крупномасштабных когерентных вихрей, которые возникают вследствие обратного каскада энергии в двумерной турбулентности. Эти вихри наблюдались ранее как в численном счете, так и экспериментально. Однако в последние годы в этой области произошел настоящий прорыв. Современные вычислительные мощности позволили сделать беспрецедентный численный счет, направленный на детальное изучение внутренней структуры таких вихрей, и на основании полученных результатов была построена асимптотическая теория, предсказывающая пространственный профиль завихренности и статистику флуктуаций на его фоне внутри когерентных вихрей (один из немногих точных аналитических результатов в теории развитой турбулентности после классических работ А. Н. Колмогорова).
Ключевые работы:
A.N. Doludenko, S.V. Fortova, I.V. Kolokolov, V.V. Lebedev, Coherent vortex in a spatially restricted two-dimensional turbulent flow in absence of bottom friction, Physics of Fluids 33, 011704 (2021); [LINK]
I. Kolokolov, V. Lebedev, Structure of coherent vortices generated by the inverse cascade of two-dimensional turbulence in a finite box, Phys. Rev. E 93, 033104 (2016); [LINK]
J. Laurie, G. Boffetta, G. Falkovich, I. Kolokolov, V. Lebedev, Universal Profile of the Vortex Condensate in Two-Dimensional Turbulence, Phys. Rev. Lett. 113, 254503 (2014); [LINK]
Геострофические вихри во вращающейся жидкости
Сильное вращение делает турбулентное течение квази-двумерным, что приводит к передачи энергии вверх по масштабам. Недавние численные эксперименты показывают, что при определенных условиях энергия накапливается на масштабе равном размеру системы, формируя когерентные вихревые структуры также известные как конденсат. Мы аналитически описали взаимодействие сильного конденсата со слабыми мелкомасштабными турбулентными пульсациями и получили уравнение, которое позволяет определить радиальную скорость когерентного вихря. При быстром внешнем вращении профили скоростей циклонов и антициклонов идентичны друг другу. По мере уменьшения внешнего вращения эта симметрия исчезает: максимальная скорость в циклонах больше, а положение максимума ближе к оси вихря по сравнению с антициклонами. Кроме того, наш анализ показывает, что размер антициклона не может превышать определенного критического значения, которое зависит от чисел Россби и Рейнольдса. Максимальный размер циклонов ограничен только размером системы при тех же условиях. Наши предсказания основаны на линейной эволюции турбулентных пульсаций на фоне когерентного вихревого течения и сопровождаются оценками, вытекающими из нелинейного уравнения Навье-Стокса.
Ключевые работы:
D.D. Tumachev, S.V. Filatov, S.S. Vergeles, A.A. Levchenko, Two Dynamical Regimes of Coherent Columnar Vortices in a Rotating Fluid, JETP Letters 118(6), 426-432 (2023); [LINK]
V.M. Parfenyev, S.S. Vergeles, Influence of Ekman friction on the velocity profile of a coherent vortex in a three-dimensional rotating turbulent flow, Phys. Fluids 33, 115128 (2021); [LINK]
I. Kolokolov, L. Ogorodnikov, S. Vergeles, Structure of coherent columnar vortices in three-dimensional rotating turbulent flow, Phys. Rev. Fluids 5, 034604 (2020); [LINK]
Генерация вихревых течений поверхностными волнами
Поверхностные волны, распространяющиеся под углом друг к другу, генерируют горизонтальное вихревое течение вследствие гидродинамической нелинейности в вязкой жидкости. Горизонтальная геометрическая структура индуцированного течения совпадает со структурой стоксового дрейфа в идеальной жидкости, но его стационарная амплитуда и глубина проникновения в неограниченной системе больше при малом угле между волнами. Генерация вихревого течения происходит в тонком вязком подслое вблизи поверхности жидкости, а распространение в объем происходит диффузионным образом за счет вязкости. В природе поверхность жидкости обычно загрязнена, что в первом приближении можно смоделировать наличием тонкой жидкой эластичной нерастворимой пленки. В этом случае амплитуда вихревого течения параметрически усиливается, причем параметром является добротность поверхностных волн. Построенная теория находится в количественном соответствии с результатами лабораторных экспериментов.
Ключевые работы:
V. Parfenyev, S. Filatov, M. Brazhnikov, S. Vergeles, A. Levchenko, Formation and decay of eddy currents generated by crossed surface waves, Phys. Rev. Fluids 4, 114701 (2019); [LINK]
V. Parfenyev, S. Vergeles, Influence of a thin compressible liquid film on the eddy currents generated by interacting surface waves, Phys. Rev. Fluids 3, 064702 (2018); [LINK]
S. Filatov, V. Parfenyev, S. Vergeles, M. Brazhnikov, A. Levchenko, V. Lebedev, Nonlinear generation of vorticity by surface waves, Phys. Rev. Lett. 116, 054501 (2016); [LINK]